John Watrous 《Introduction to the Theory of Computing》13 -- 图灵机的变体

前言

这节课我们将会继续讨论图灵机模型，着重于讲改变模型而又不影响它们能力的方法。

知识点

图灵机的简单变体

没必要过于纠结我们上节课提到的关于DTM的特殊定义。实际上，如果你看两本不同的计算理论书籍，你很有可能看到两个图灵机定义在一个或者多个方面不同。
　　比如，我们讨论的定义指定图灵机的磁带在两个方向上都是无限的，但是有时候人们定义模型时往往会指定磁带的右边是无限的。自然地，如果磁带上存在一个最左边的区块，那么定义要明确指定图灵机在这一点上如何往左移动。也许图灵机在磁头将要移出左边界时会立马拒绝，或者也只是简单地停留在最左边的磁带区块上。
　　另外一个例子是关于磁头移动的。我们的定义声明了中磁头只能往左或往右移动，而某些图灵机定义允许磁头保持不动。通常我们也会想到图灵机可能有多个磁带的情况，并且我们确实会简短地讨论这种图灵机变体。

允许磁头不动的DTM

让我们从上面提到的一个简单变体开始，它的设计者允许磁头经过一个步骤后位置保持不变。这是对图灵机定义的一个非常小的改动，但这也是我们第一个例子，所以我们尽量讲得详细一点（也许会超过它所需要的程度）。
　　如果一个DTM的磁头被允许位置不变，以前的转移函数形式

$\delta:Q\setminus\{q_{acc},q_{rej}\}\times\Gamma\rightarrow Q\times\Gamma\times\{\leftarrow,\rightarrow\},\tag{13.1}$

将不再使用，我们将其改变为

$\delta:Q\setminus\{q_{acc},q_{rej}\}\times\Gamma\rightarrow Q\times\Gamma\times\{\leftarrow,\downarrow,\rightarrow\},\tag{13.2}$

其中向下的箭头表示磁头不移动。特别地，如果处于$\delta(p,a)=(q,b,\downarrow)$的情况，那么无论何时图灵机处于状态$p$并且磁头停留在包含符号$a$的区块，它都会将$a$重写为$b$，改变状态为$q$，并且不改变磁头的位置。
　　为了更明确一点，跟上节课中的普通DTM模型区别，让我们给这个模型另取一个名字。特别地，我们将会定义固定-磁头-DTM是一个7-元组

$M=(Q,\Sigma,\Gamma,\delta,q_0,q_{acc},q_{rej}),\tag{13.3}$

其中元组的每个部分都和普通DTM相同，除了转移函数$\delta$的形式（13.2）。
　　现在，如果我们想要给出一个固定-磁头-DTM接受和拒绝的正式定义，我们当然会这么做。这需要我们上节课中产出映射的定义，因为对于某个$p\in Q$和$a\in\Gamma$，我们需要考虑到$\delta(p,a)=(q,b,\downarrow)$这种情况。实际上这很简单 — 我们只需要将下面这个第三条规则加入到普通DTM产出映射的定义即可：

保持不动。对于每个$p\in Q\setminus\{q_{acc},q_{rej}\}、q\in Q$和$a、b\in\Gamma$满足 $\delta(p,a)=(q,b,\downarrow),\tag{13.4}$ 产出映射对于所有的$u\in\Gamma^{*}\setminus\{\sqcup\}\Gamma^{*}$和$v\in\Gamma^{*}\setminus\Gamma^{*}\{\sqcup\}$存在： $u(p,a)v\vdash_M u(q,b)v.\tag{13.5}$

　　正如我们前天提到的，允许磁头不同的情况下并没有实际改变图灵机模型的计算能力。讨论这个问题的标准方式是通过模拟技术。一个标准的DTM不能让他的磁头固定，所以他的行为不能和固定-磁头-DTM一样，但是我们用普通DTM来模拟磁头固定的情况 — 比如通过将磁头向左移动后再向右移回来，我们获得的输出将会和磁头固定的情况一样。自然地，这要求我们记录下往左移动后需要向右移回来的状态，但是这点要求并不困难。
　　更确切地说，如果

$M=(Q,\Sigma,\Gamma,\delta,q_0,q_{acc},q_{rej})\tag{13.6}$

是一个固定-磁头-DTM，那么我们可以用一个普通DTM

$K=(R,\Sigma,\Gamma,\eta,q_0,q_{acc},q_{rej})\tag{13.7}$

模拟如下：

对于$M$中每个状态$q\in Q$，$K$的状态集合$R$将会包含$q$，也包含这个状态的副本，我们记作$q’$。状态$q’$的直观意义是它表明$K$需要将磁头向右移动一个区块，然后进入状态$q$。
$K$的转移函数$\eta$的定义是 $\eta(p,a)\begin{cases}(q,b,\leftarrow)&if\ \ \delta(p,a)=(q,b,\leftarrow) \\ (q,b,\rightarrow)&if\ \ \delta(p,a)=(q,b,\rightarrow) \\ (q',b,\leftarrow)&if\ \ \delta(p,a)=(q,b,\downarrow)\end{cases}\tag{13.8}$ 其中$p\in Q\setminus\{q_{acc},q_{rej}\}$和$a\in\Gamma$，还有 $\eta(q',c)=(q,c,\rightarrow)\tag{13.9}$ 其中$q\in Q$和$c\in\Gamma$。

　　使用图标来书面表达，我们可以如下描述这个模拟过程。假设固定-磁头-DTM $M$的一个转移状态图是这样：

那么$K$的状态图就会将这个转移替换如下：

这里，从$q’$到$q$的转移包括了每个磁带符号$c\in\Gamma$。同样的状态$q’$可以安全地使用在磁头固定转移到$q$的操作上。
　　不难看出$K$的计算将会直接模仿$M$的计算。DTM $K$也许运行起来更花时间，因为有时候$M$只需要一步的操作，它会需要两步，但是这并不是我们需要关心的。这里的底线是每个通过一个固定-磁头-DTM可判定或者半可判定的语言也可以通过一个普通DTM可判定或者半可判定。
　　换个方向就很平凡了：一个固定-磁头-DTM可以轻松模拟一个普通DTM，只要不使用磁头固定操作即可。因此，两个模型时等价的。
　　这样，如果某些情况下需要你做决定，使用固定-磁头-DTM会更方便，你可以转换到这个模型 — 并且通过观察我们刚才证明的等价性，你能得出一些关于普通DTM模型的有趣结论。
　　然而实际上刚才讨论的固定-磁头-DTM并不是我们抛弃普通DTM模型的重点 — 我们之所以详细叙述这个等价性仅仅是因为他是我们第一个例子，往后就没有什么需要特别提到固定-磁头-DTM机会了。

多轨磁带DTM

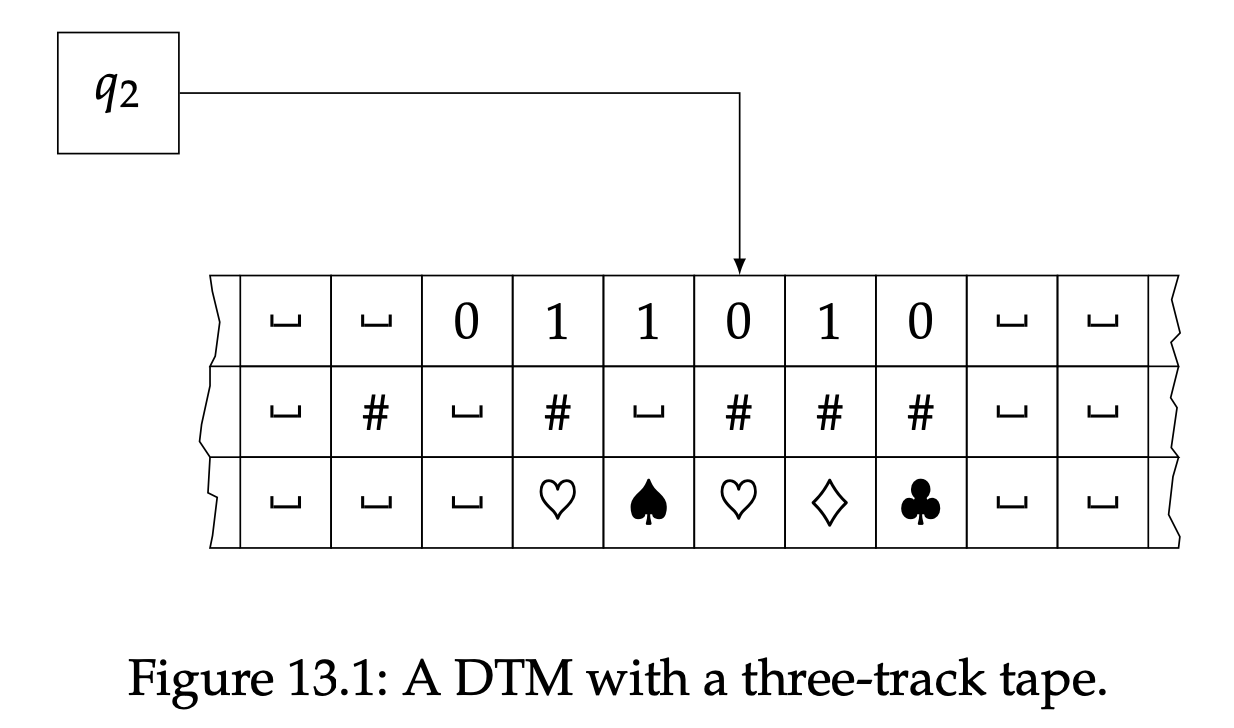
另外一个有用的DTM变体的不同之处在于它的磁带有多条轨道，如图13.1所示。更具体地说，我们也许要假设磁带上有$k$个轨道，$k$是一个正整数，每个磁头位置都能定位到$k$个分开的存储着一个符号的磁带区块。允许$k$个不同的轨道拥有不同的磁带字母表$\Gamma_1,…,\Gamma_k$是很有用的。当磁头扫描磁带上某个位置时，他能高效读取并且同时改变磁头定位的所有轨道区块的存储的符号。
　　比如，就拿图13.1来说，这个DTM的第一个轨道上的磁带字母表是$\Gamma_1=\{0,1,\sqcup\}$，第二个轨道上的磁带字母表是$\Gamma_2=\{\sharp,\sqcup\}$，第三个轨道上的磁带字母表是$\Gamma_3=\{\clubsuit,\heartsuit,\diamondsuit,\spadesuit,\sqcup\}$。
　　实际上开起来这根本不是一个DTM定义上的变体 — 他只是一个普通DTM，而它的字母表$\Gamma$是一个笛卡尔积产物

$\Gamma=\Gamma_1\times\cdots\times\Gamma_k.\tag{13.10}$

任意DTM的磁带字母表都由输入字母表加上一个空格符号组成，所以我们可以将输入字母表符号$\sigma\in\Sigma$区别于磁带符号$(\sigma,\sqcup,…,\sqcup)$，并且我们也会把$(\sqcup,…,\sqcup)$当做是多轨DTM上的空格符号。

磁带单向无限的DTM

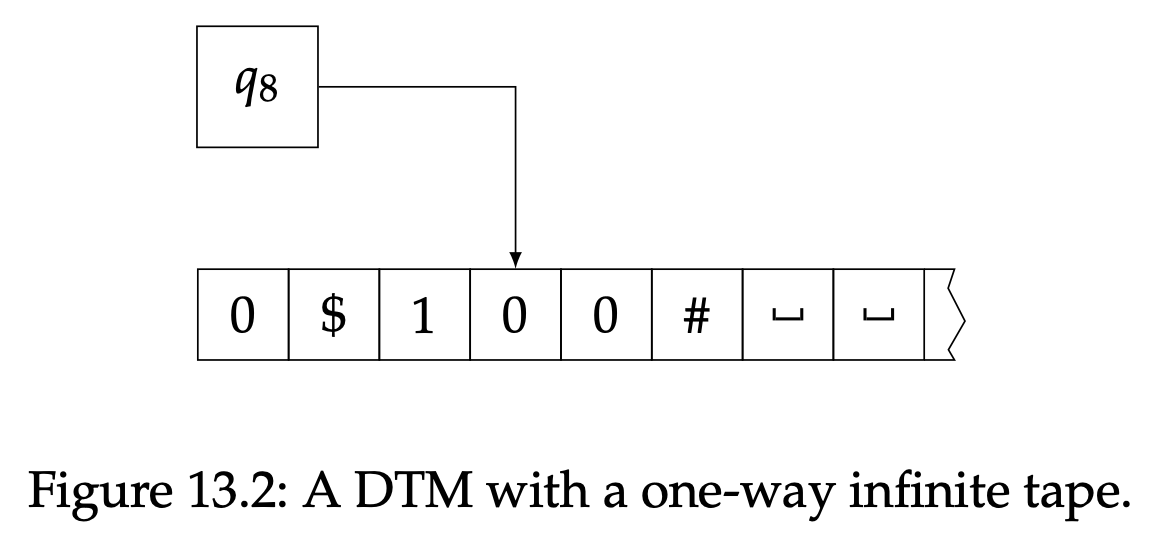
磁带单向无限的DTM在之前讲到DTM的磁带是双向无限时提到过。图13.2阐述了这样一个DTM。让我们说明一下，如果DTM的磁头在最左侧的区块上尝试往左移动，它的磁头位置会保持不变，但是计算正常进行 — 这种情况下也许会发出一种不愉快的卡带声音。
　　我们使用普通的DTM（磁带双向无限）就能很简单地模拟磁带单向无限的DTM。例如，我们可以放置一个特殊符号，比如剪刀符号，在双向无限的磁带计算开始的地方，也就是在输入的左侧。普通的DTM运作起来就会和磁带单向无限的DTM一样，但是如果磁头在计算过程中扫描到了剪刀符号，它会往右移动一个区块并且不改变状态。

这个图恰好模仿了如上所述的磁带单向无向的DTM。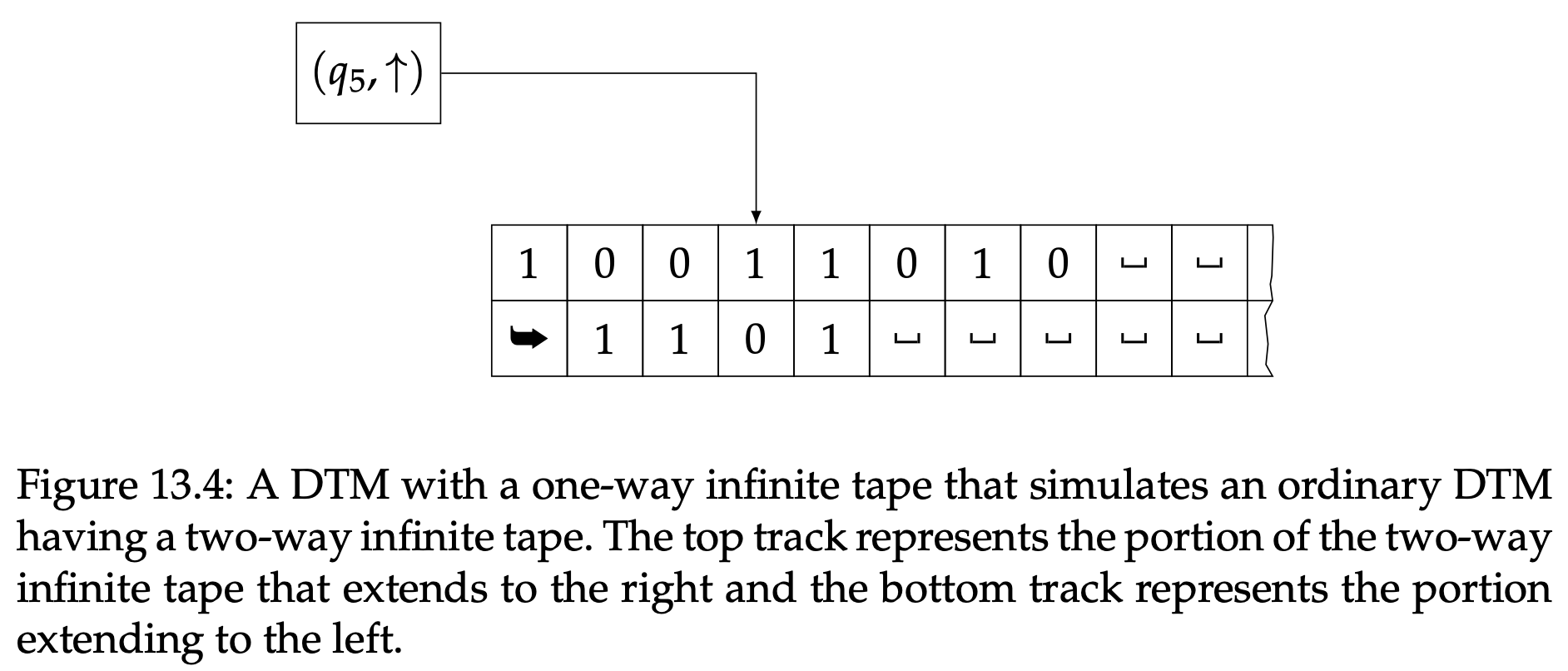

　　使用一个磁带单向无限的DTM模仿普通DTM相对来说就比较有挑战性了，但是并不困难。很容易想到两种自然方式。第一种如图13.4所示。本质上，双轨道磁带单向无限的DTM可以用来模拟普通DTM，看起来就像磁带对折了一样。有限状态控制器记录被模拟的DTM的状态，这个DTM记录着存储被扫描符号存储的磁带。一个特殊符号，比如回车符号，会被放在第一个区块靠近下边的位置上来辅助模拟。
　　第二种模拟方式不需要两条轨道，而是需要一些更多的步骤，因此会影响效率。一个特殊符号会被放在单向无限磁带的最左侧区块上，当这个符号被扫描到时，DTM会执行一个子程序，磁带上每个符号都会向右移动一个区块，为了在左边给一个新的区块“留下控件”。当然我们还需要使用一个特殊符号来标记磁带最右侧的非空格符号，这样转移小程序才能完成 — 否则我们将不知道每个（非空格）符号是么时候右移了一个区块。

多磁带图灵机

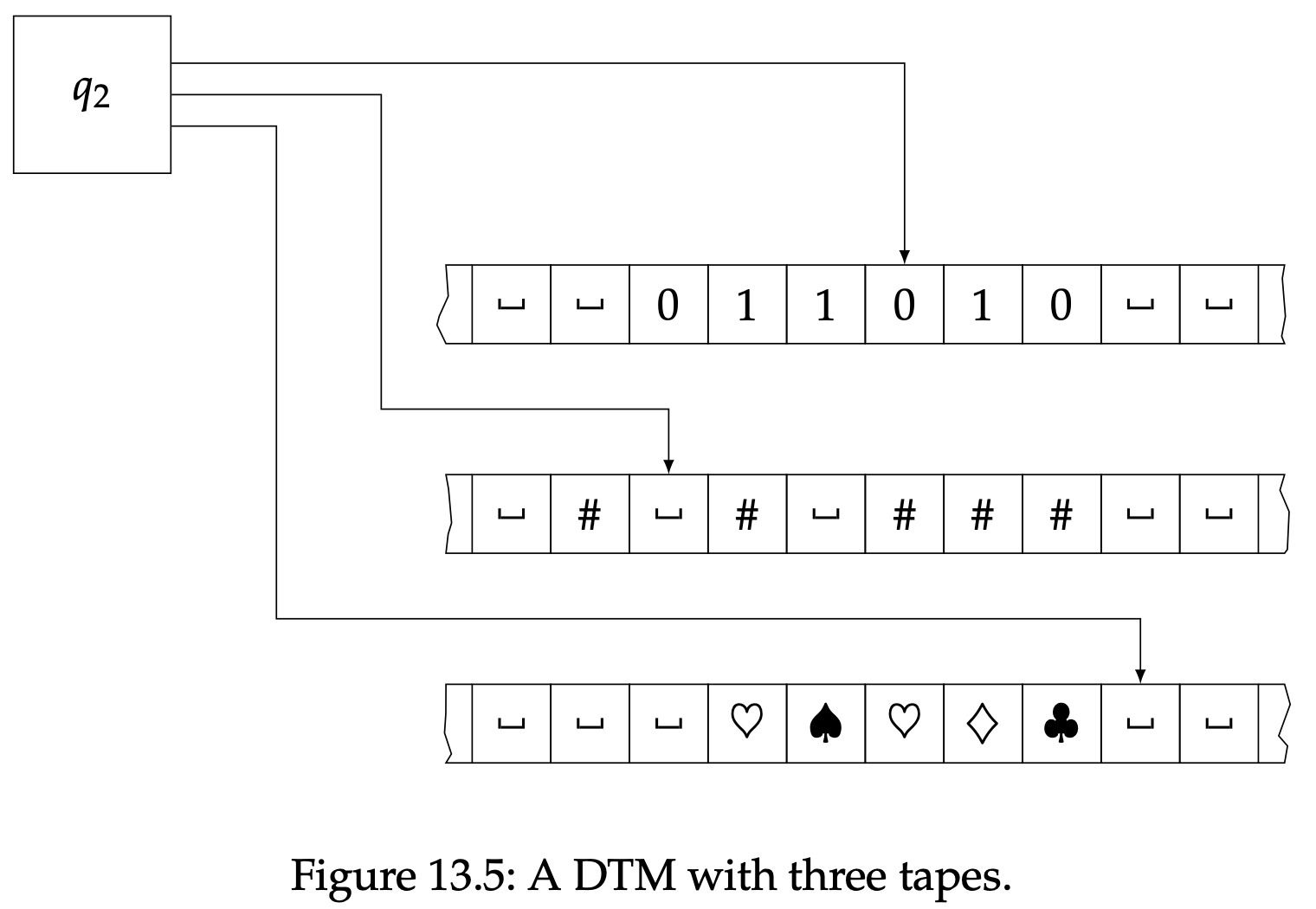
最后一种图灵机模型变体非常有用。一个多磁带DTM和普通（单磁带）DTM运行起来类似，除了它由$k$个磁头独立运作在$k$个磁带上，$k$是一个正整数。例如，图13.5阐述了一个三条磁带的多磁带DTM。
　　一般来说，一个$k$-磁带DTM的定义和普通DTM是类似的，除了转移函数的形式稍微复杂一点。具体一点，如果一个$k$-磁带DTM的磁带字母表是$\Gamma_1,…,\Gamma_k$，那么转移函数的形式就是：

$\delta:Q\setminus\{q_{acc},q_{rej}\}\times\Gamma_1\times\cdots\times\Gamma_k\rightarrow Q\times\Gamma_1\times\cdots\times\Gamma_k\times\{\leftarrow,\downarrow,\rightarrow\}^k\tag{13.11}$

如果我们做一个简单的假设，每条磁带使用的字母表都一样（模型并没有限制这一点，就像我们可总是能将单磁带字母表表示成多个字母表的并集$\Gamma=\Gamma_1\cup\cdots\cup\Gamma_k$），转移函数的形式为

$\delta:Q\setminus\{q_{acc},q_{rej}\}\times\Gamma^k\rightarrow Q\times\Gamma^k\times\{\leftarrow,\downarrow,\rightarrow\}^k\tag{13.12}$

（两种情况都允许磁头位置保持不变。自然地你也可以假设一种变体，它的每一步都需要磁头移动，但是我们考虑多磁带DTM时也会允许磁头位置保持不变 — 因为这样会更灵活普遍，能简单执行一些复杂的计算。）形如13.12的转移函数的解释如下。如果存在

$\delta(p,a_1,...,a_k)=(q,b_1,...,b_k,D_1,...,D_k),\tag{13.13}$

那么如果DTM处于状态$p$，正在读取$k$条磁带上的符号$a_1,…,a_k$，那么

当前状态改变为$q$，
在$k$条磁带上写入符号$b_1,…,b_k$（重写符号$a_1,…,a_k$），以及
第$j$条磁带的磁头移动或者保持不变取决于$D_j\in\{\leftarrow,\downarrow,\rightarrow\}$，其中$j=1,..,k$。

　　有一种使用单磁带DTM模仿多磁带DTM的方式是将$k$个磁带内容和磁头位置的信息存储在多轨单磁带上。例如，图13.5的多磁带DTM配置可以用图13.6的单磁带DTM来表示。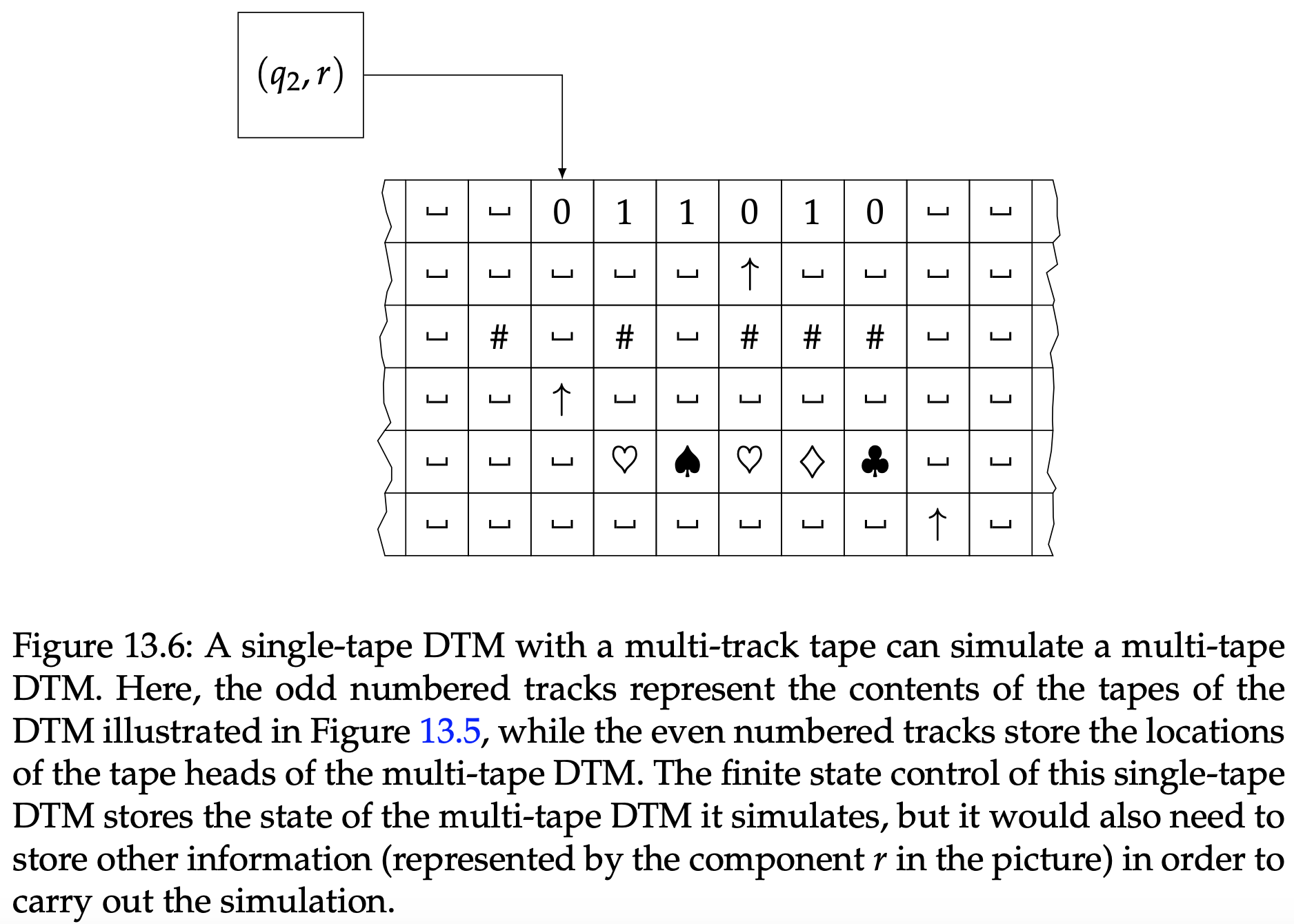

　　自然地，一个这样的模拟需要单磁带DTM使用很多步骤来模仿多磁带DTM。让我们用$K$来之带多磁带DTM，$M$来指代单磁带DTM。为了模仿$K$中的一个步骤，DTM $M$需要许多步骤：首先为了确定$K$的$k$个磁头所扫描的符号，它必须整体扫描磁带，并且将这些符号存储在优先状态控制器中。一旦知道了所有符号，它就能确定$K$采取的是什么行动，然后实现这个行动 — 这也表示为了更新轨道上存储的关于$K$的磁带内容和磁头信息，磁头位置可能会移动，需要再次整体扫描磁带。要把这些详细写下来会很复杂，而且有许多具体的方式能将这个普遍思路实现 — 但是只要有足够的时间和冬季，用这种方式给出一个单磁带DTM $M$模拟一个已知的多磁带DTM $K$的正式定义还是可行的。

原文链接

https://cs.uwaterloo.ca/~watrous/ToC-notes/ToC-notes.13.pdf